貪婪演算法

概述

貪婪演算法(Greedy Algorithm)，意思是每次只選擇當下的最佳解，來得到最後的最佳解答案。

相較於其它演算法，這個更常概念性的出現，只要演算法的一部分滿足這樣的操作就具有貪婪演算法的性質，但貪婪演算法並非所有情況都適用。

充要條件

貪婪選擇性質

引用自 https://en.wikipedia.org/wiki/Greedy_algorithm#Specifics

Whichever choice seems best at a given moment can be made and then (recursively) solve the remaining sub-problems. The choice made by a greedy algorithm may depend on choices made so far, but not on future choices or all the solutions to the subproblem. It iteratively makes one greedy choice after another, reducing each given problem into a smaller one. In other words, a greedy algorithm never reconsiders its choices. This is the main difference from dynamic programming, which is exhaustive and is guaranteed to find the best (that is, the ‘optimal’) solution. After every stage, dynamic programming makes decisions based on all the decisions made in the previous stage and may reconsider the previous stage’s algorithmic path to the solution.

這段話的白話文是 當下做出的局部最佳選擇必定包含在最佳解之中，做出最佳選擇後不再需要回溯只需要往下解決子問題就能得出最佳解的情況。

若要確實的證明滿足貪婪選擇性質的話常用交換論證以及擬陣

最佳子結構

該問題的最佳解是由各個子問題的最佳解所構成的

範例說明

1. 排程問題

說明：盡可能選擇最多的任務，並且時間不能重疊

     start, end
任務 A: [5, 9]
任務 B: [1, 2]
任務 C: [3, 4]
任務 D: [0, 6]
任務 E: [5, 7]
任務 F: [8, 9]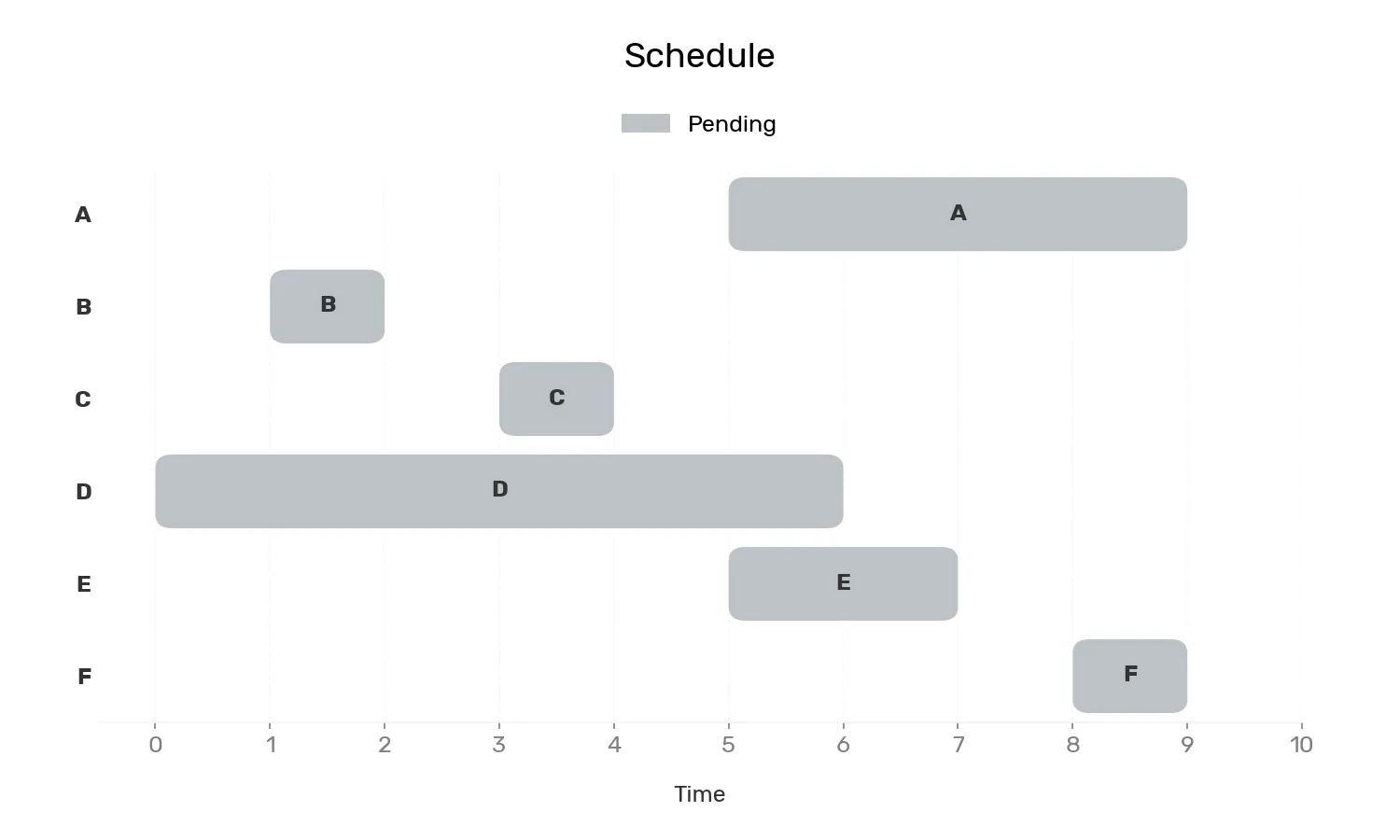

如圖所示，要選擇最多的區塊但不能重疊，使用貪婪演算法將最早完成的當作當前最佳解

1. 選擇當前最早完成的 B [1, 2]

   

2. 接著從2開始，下一個起始時間>=2並且不重疊的是 C [3, 4]

   

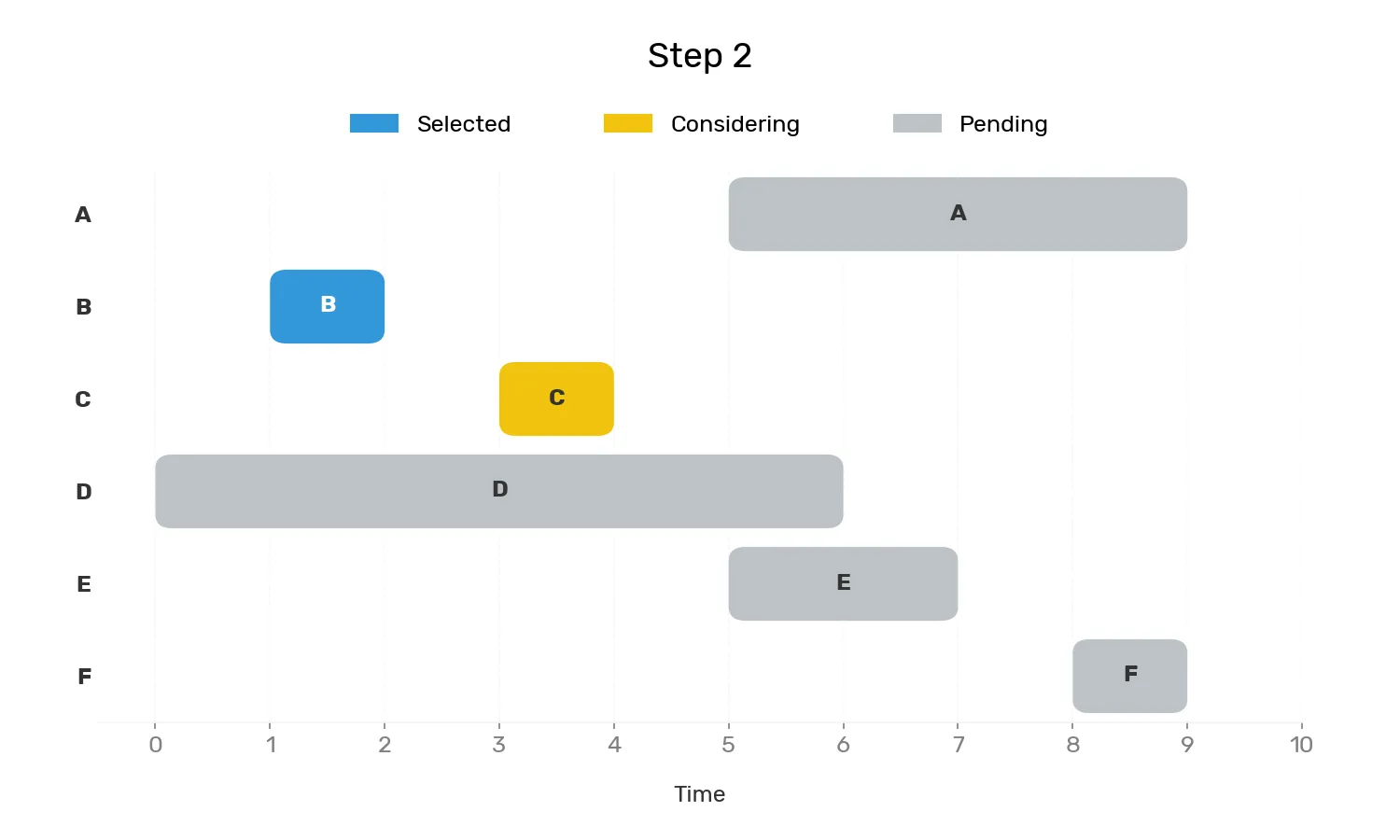
3. 接著從4開始，下一個起始時間>=4並且不重疊的是 E [5, 7]

   

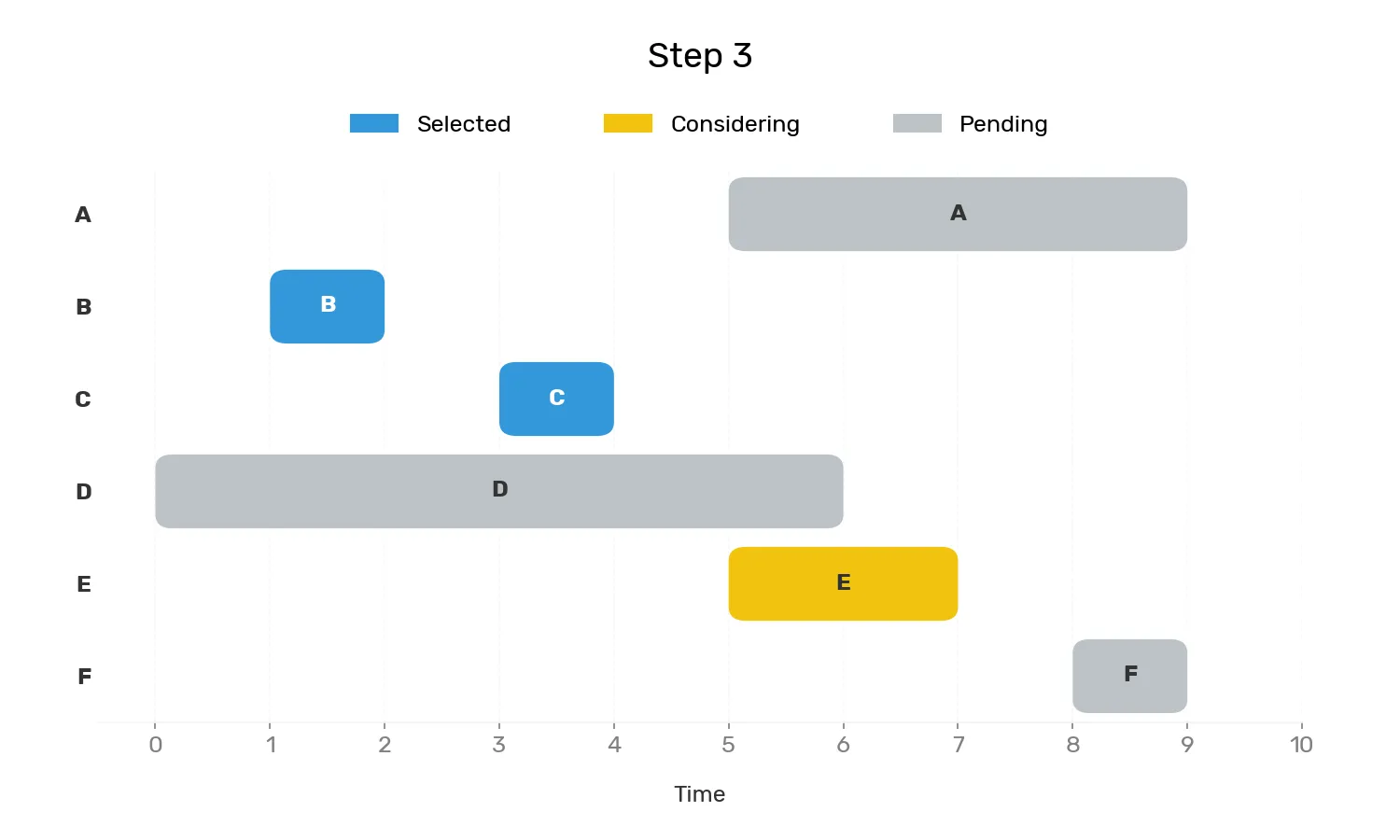
4. 接著從7開始，下一個起始時間>=7並且不重疊的是 F [8, 9]

   

5. 完成，一共選取了$O = [B, C, E, F]$

   

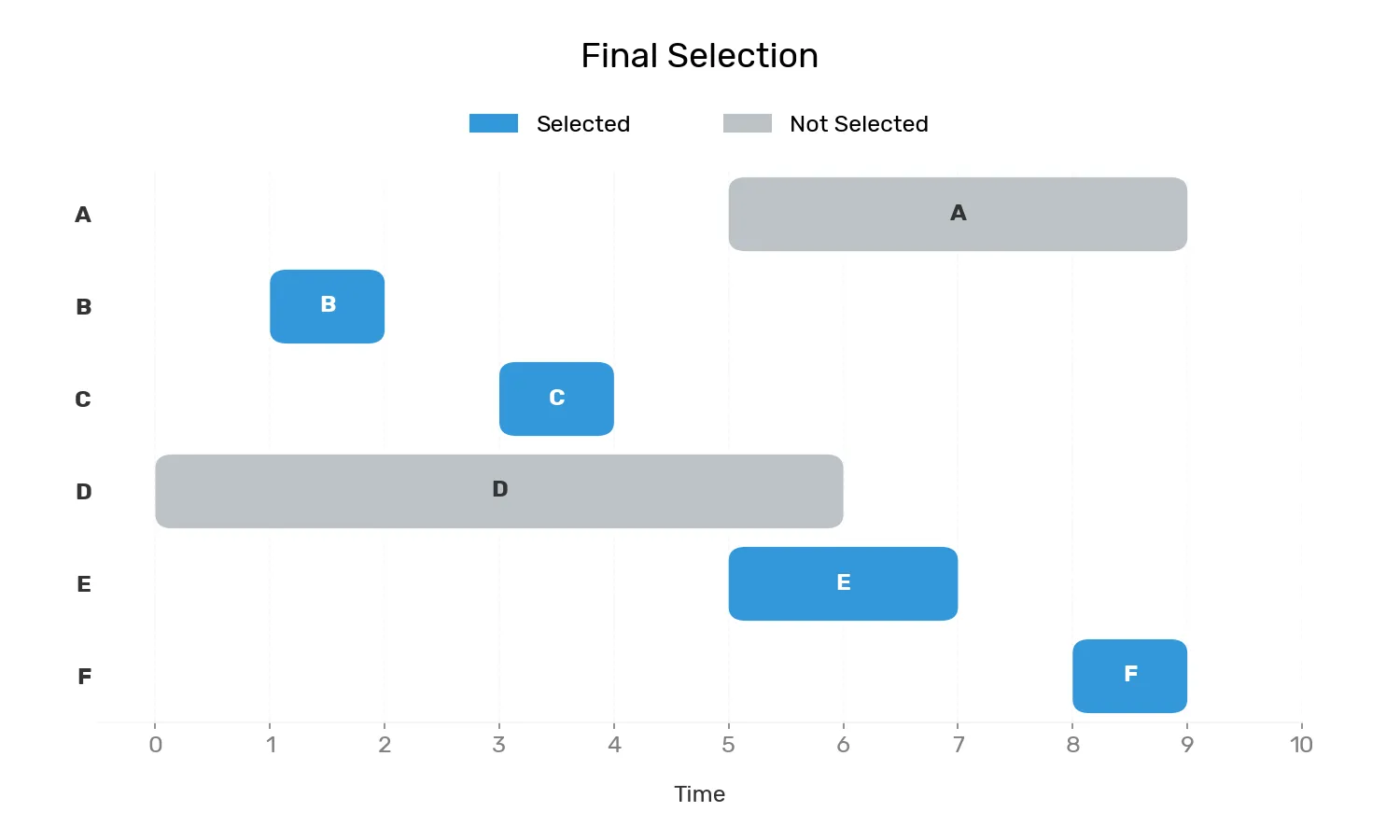
使用交換論證說明其符合貪婪選擇性質

• 所有任務 $S = \{A, B, C, D, E, F\}$
• 選擇最早完成的 $g_1$ ( B [1, 2] )
• 假設存在一個最佳解 $O = \{o_1, o_2, ..., o_k\}$
• 假設最佳解 $O$ 不包含 $g_1$
• 那麼 $O$ 也有自己的第一個 $o_1$，$o_1 \neq g_1$
• 根據策略選擇最早結束的，$g_1$的完成時間必然小於等於 $o_1$，$Finish(g_1) \le Finish(o_1)$
• 新的集合 $O' = (O - \{o_1\}) \cup \{g_1\}$
• $O'$ 與 $O$ 同樣有 $k$ 個任務
• $O'$ 與 $O$ 裡面的其它任務 $\{o_2, ..., o_k\}$ 是相容的，因為 $Finish(g_1) \le Finish(o_1)$
• 這表示 $g_1$ 也可以和 $O$ 裡的任務相容並且數量相同，$O'$ 是一個有效的解

說明其符合最佳子結構
當選擇了 B [1, 2] 現在可以視為是一個起始點是2的新題目
當選擇了 C [3, 4] 現在可以視為是一個起始點是4的新題目
當選擇了 E [5, 7] 現在可以視為是一個起始點是7的新題目
當選擇了 F [8, 9] 現在可以視為是一個起始點是9的新題目
每次選擇都是一個新的子問題，將這些子問題合併起來就是最終的結果 $O = [B, C, E, F]$

我們再來看看別的例子

2. 湊幣問題_1

說明：在硬幣 $S = \{1, 3, 4\}$ 中使用最少的硬幣湊成剛好的幣值 $N$
就是平時付錢的行為，使用貪婪演算法每次選擇最大的面額

使用交換論證說明其符合貪婪選擇性質

• 硬幣幣值 $S = \{1, 3, 4\}$
• 尋找一個大於 $4$ 的臨界點檢驗，假設目標金額 $N = 6$
• 最佳解 $O = \{3, 3\}$，使用硬幣數量 $k = 2$
• 若貪婪選擇性質成立，存在一個最佳解 $O' \supseteq \{4\}$
• $N = 6$，所以 $O'$ 還需要補足 $2$，湊出 $2$ 需要 $\{1, 1\}$
• $O' = \{4, 1, 1\}$ 的硬幣數量 $k' = 3$，$k' > k$，貪婪選擇性質不成立

說明其符合最佳子結構
假設初始 $N = 6$
當選擇了最大幣值 $4$ 現在可以視為新題目 $N = 2$
當選擇了最大幣值 $1$ 現在可以視為新題目 $N = 1$
當選擇了最大幣值 $1$ 現在可以視為新題目 $N = 0$

這個幣值不符合 貪婪選擇性質 但符合 最佳子結構，所以能用動態規劃(Dynamic programming)解決，該章節正在撰寫中

3. 湊幣問題_2

說明：在硬幣 $S = \{1, 5, 10, 50\}$ 中使用最少的硬幣湊成剛好的幣值 $N$
使用貪婪演算法每次選擇最大的面額

使用交換論證說明其符合貪婪選擇性質

• 硬幣幣值 $S = \{1, 5, 10, 50\}$
• 尋找一個大於 $50$ 的臨界點檢驗，假設目標金額 $N = 60$
• 假設最佳解 $O$ 不包含 $50$，$O = \{10, 10, 10, 10, 10, 10\}$，使用硬幣數量 $k = 6$
• 若貪婪選擇性質成立，存在一個最佳解 $O' \supseteq \{50\}$
• $N = 60$，所以 $O'$ 還需要補足 $10$，湊出 $10$ 需要 $\{10\}$
• $O' = \{50, 10\}$ 的硬幣數量 $k' = 2$，$k'(2) < k(6)$，符合結果

實際需要從最小測試到 $\max(S) + \text{second\_max}(S)$ 都符合最佳解
如果 $N$ 遠大於 $\max(S)$，則最佳解必定包含 $\max(S)$，如同縮減成子問題的概念
而 $\max(S) + \text{second\_max}(S)$ 之內可能產生複雜的交互作用。

說明其符合最佳子結構
假設初始 $N = 60$
當選擇了最大幣值 $50$ 現在可以視為新題目 $N = 10$
當選擇了最大幣值 $10$ 現在可以視為新題目 $N = 0$

補充

貨幣幣值是經過安排的符合標準，所以我們平時湊錢的方式總是符合預期，這篇文章提到了新增幣值時確保符合貪婪解法的定理。

實際解題通常不搞麻煩的證明貪婪演算法有效，可以判斷規模 $O$ 與 $10^8$ 的關係、想個測資反例、實際嘗試等方式來猜測有效性。