Big-O 複雜度評估

概述

大O符號用來衡量一個演算法，對於能直接影響執行次數的輸入值n評估且忽略所有常數項，評估執行的時間和占用記憶體的效率

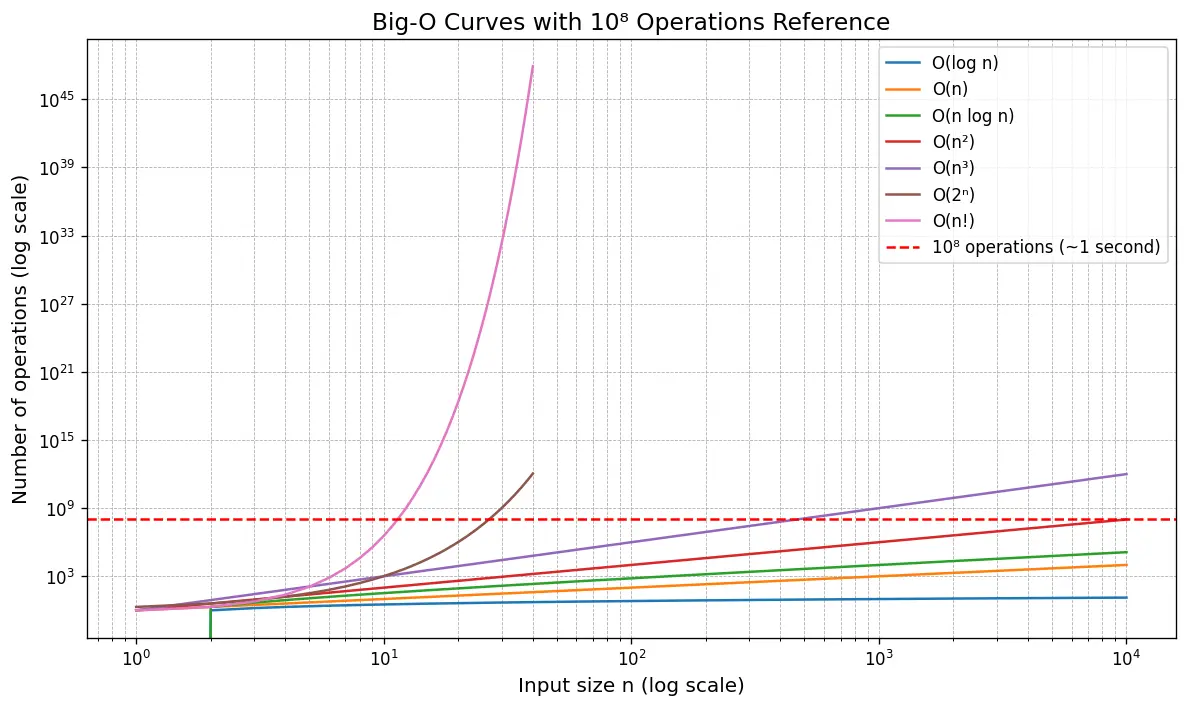常見的量級有上圖這些，解題的時間要求標準是1秒，大約在10的8次方
比如輸入值n的上限是10^8的話通常會有O(n)或更優的解，使用O(n²)的話會超時
Big-O在實務上理解代碼就能大致知道在哪一個量級，特定的演算法在網路上可查詢，本篇不做數學式的說明。

時間複雜度

O(1)

常數時間，輸入內容不影響程式執行步數

O(log n)

log在這裡一般默認以2為底，常見的二分搜尋就是O(log n)

二分搜尋法

針對已排序的資料每次找中間點的方式來找內容

說明：
例如從 1~100 找一個數字：

1. 第一次找 50
2. 如果目標 > 50 → 在 51~100 中間找 75
3. 如果目標 > 75 → 在 76~100 中間找 87
4. 重複以上過程直到找到目標

範例：
一個已排序的陣列 arr 判斷是否存在內容 item

C++

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

// 手寫版 - 可自行練習
bool BinarySearch(const vector<int>& arr, int item) {
    int left = 0;
    int right = arr.size() - 1;

    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (arr[mid] == item) {
            return true;
        } else if (arr[mid] < item) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }
    return false;
}

int main()
{
    vector<int> arr{ 1, 2, 3, 4, 5 };
    int item = 3;
    cout << (binary_search(arr.begin(), arr.end(), item) ? "True" : "False");
}

C#

namespace ConsoleApp1
{
    internal class Program
    {
        // 手寫版 - 可自行練習
        static bool BinarySearch(int[] arr, int item)
        {
            int left = 0;
            int right = arr.Length - 1;

            while (left <= right)
            {
                int mid = left + (right - left) / 2;
                if (arr[mid] == item)
                {
                    return true;
                }
                else if (arr[mid] < item)
                {
                    left = mid + 1;
                }
                else
                {
                    right = mid - 1;
                }
            }
            return false;
        }

        static void Main(string[] args)
        {
            int[] arr = [1, 2, 3, 4, 5];
            int item = 3;
            Console.WriteLine(Array.BinarySearch(arr, item) >= 0);
        }
    }
}

何時使用現成函數

每個語言都已經寫好最佳的函數做法，比如C++的sort根據內容選擇(快速排序/堆積排序/插入排序)，Java/Python使用性能非常良好的Timsort，實務上考量到性能和編寫時間，在自行練習以外不該手動寫一個功能函數，應熟悉內部函數的用法。

O(n)

常見的有線性搜尋和任何將內容循環一遍的敘述

線性搜尋

對於未排序資料，從頭到尾搜尋陣列內容

說明：
例如從1~100找一個數字，從1開始，逐一檢查每個數字，直到找到目標或結束

範例：
在未排序陣列 arr 中找到元素 item 的索引，若不存在則返回 -1

C++

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;

int main()
{
    vector<int> arr{ 12, 43, 56, 78, 9 };
    int item = 9;
    auto it = find(arr.begin(), arr.end(), item);
    if (it == arr.end()) {
        cout << -1;
        return 0;
    }
    cout << distance(arr.begin(), it);
    return 0;
}

C#

namespace ConsoleApp1
{
    internal class Program
    {
        static void Main(string[] args)
        {
            int[] arr = [12, 43, 56, 78, 9];
            int item = 9;
            Console.WriteLine(Array.IndexOf(arr, item));
        }
    }
}

Python

arr = [12, 43, 56, 78, 9]
item = 9
try:
    print(arr.index(item))
except ValueError:
    print(-1)

O(n log n)

基本的快速排序法的平均複雜度，不過快速排序在極端情況比如資料已經排序好的時候最壞情況是O(n²)

快速排序法

快速排序法是一種當前常見的排序演算法

說明：

1. 選擇一個基準值(pivot)
2. 所有比pivot小的放在它前面，比pivot大的放在後面
3. 分別對pivot的左右兩邊重複上述動作，直到子陣列長度<=1

範例：
使用c++的內建的快速排序法，將陣列 arr 遞增排序

C++

#include <iostream>
#include <algorithm>
#include <functional>
using namespace std;

int main()
{
    // qsort是c函數，比較函數的參數型別較複雜，c++可直接用sort()做非指定排序
    int arr[] = { 5, 2, 9, 1, 5, 6 };
    qsort(arr, sizeof(arr) / sizeof(arr[0]), sizeof(int), [](const void* a, const void* b) {return *(int*)a - *(int*)b; });
    return 0;
}

O(n²)

常見的有泡沫排序法，但是兩層for循環n就是最明顯的n²樣式

泡沫排序法

泡沫排序法是一種較慢的排序法，適合學習用途

說明：

1. 循序讀取陣列一遍，將兩兩相鄰內容比較
2. 如果前面大於後面，則交換它們 (遞增)
3. 重複以上內容直到沒交換過

範例：
使用泡沫排序法將長度為 n 的陣列 arr 遞增排序

C++

#include <iostream>
using namespace std;

int main()
{
    int arr[] = { 5, 2, 9, 1, 5, 6 };
    int n = sizeof(arr) / sizeof(arr[0]);
    bool swap = true;
    while (swap) {
        swap = false;
        for (int i = 1; i < n; i++) {
            if (arr[i - 1] > arr[i]) {
                int temp = arr[i];
                arr[i] = arr[i - 1];
                arr[i - 1] = temp;
                swap = true;
            }
        }
    }
    return 0;
}

C#

namespace ConsoleApp1
{
    internal class Program
    {
        static void Main(string[] args)
        {
            int[] arr = [5, 2, 9, 1, 5, 6];
            int n = arr.Length;
            bool swap = true;
            while (swap)
            {
                swap = false;
                for (int i = 1; i < n; i++)
                {
                    if (arr[i - 1] > arr[i])
                    {
                        int temp = arr[i];
                        arr[i] = arr[i - 1];
                        arr[i - 1] = temp;
                        swap = true;
                    }
                }
            }
        }
    }
}

O(n³)

主要有矩陣乘法以及三層迴圈n的東西，比如佛洛依德演算法

Floyd-Warshall演算法

佛洛依德演算法用於取得任意兩點間的最短路徑

說明：
涉及後面會提到的圖論，這邊只說明關鍵內容
如果 i 到 j 的距離比 i 到 k，k 再到 j 的距離還大，則將 i 到 j 的距離更新成 i 到 k 到 j

範例：
Floyd-Warshall的核心代碼

C++

for(int i = 0; i < n; i++) {
    for(int j = 0; j < n; j++) {
        for(int k = 0; k < n; k++){
            if (dist[i][j] > dist[i][k] + dist[k][j]) {
                dist[i][j] = dist[i][k] + dist[k][j];
            }
        }
    }
}

O(n!)

全排列以及一些暴力解

全排列

說明：
將陣列的內容按順序將全部可能的排列方式輸出

範例：
使用python的itertools的排列函數permutations生成

Python

import itertools

arr = [1, 2, 3]
print(*itertools.permutations(arr))
/*
(1, 2, 3) (1, 3, 2) (2, 1, 3) (2, 3, 1) (3, 1, 2) (3, 2, 1)
*/

空間複雜度

空間複雜度較簡單，將數據大小乘以使用數量就是實際用量，比如 n = 1024 建立一個 int arr[n] 就是用了4 bytes × 1024 = 4096 bytes

在編寫代碼時一般會將使用的陣列大小宣告好，可以明確的看出記憶體用量。